
これまで幾何公差を勉強する中でどうしても理解できなかった「最大実体公差」。
ようやくわかりやすい解説書を見つけて納得しましたが、それでも難しい考え方。
専門的な言葉をできるだけ使わずやさしく基礎から説明します。(以下書籍おすすめ)
最大実体公差とは
最大実体公差(MMC:Maximum Material Condition)とは、
「部品の体積が一番多い状態」で考える公差のルールのことです。
寸法に余裕が生まれると「ボーナス公差」が追加され、許容範囲が広がります。
基本のイメージ

穴(例:直径10±0.1mmの穴)
ドーナツはサイズが同じなら穴が小さいほど食べる部分が多い=穴が小さいほど材料の量が多いです。
小さいほど材料が多く残る → 最大実体状態は「最小径(9.9mm)」
軸(例:直径10±0.1mmの棒)
ソーセージは長さが同じなら太いほうが食べる部分が多い=棒が太いほど材料の量が多いです。
太いほど材料が多い → 最大実体状態は「最大径(10.1mm)」
- 穴は「一番小さいサイズ」がMMC
- 軸は「一番大きいサイズ」がMMC
最大実体公差を使うメリット
図面に「位置度」などの幾何公差をつけるとき、MMCを指定しておくと便利です。
なぜなら、部品がMMCから外れる(=余裕ができる)と、その分だけ公差を追加できるため。
この追加された公差を「ボーナス公差」といいます。
つまり、部品がゆるゆるになればなるほど作るのが楽になる仕組みです。
ボーナス公差の具体例①
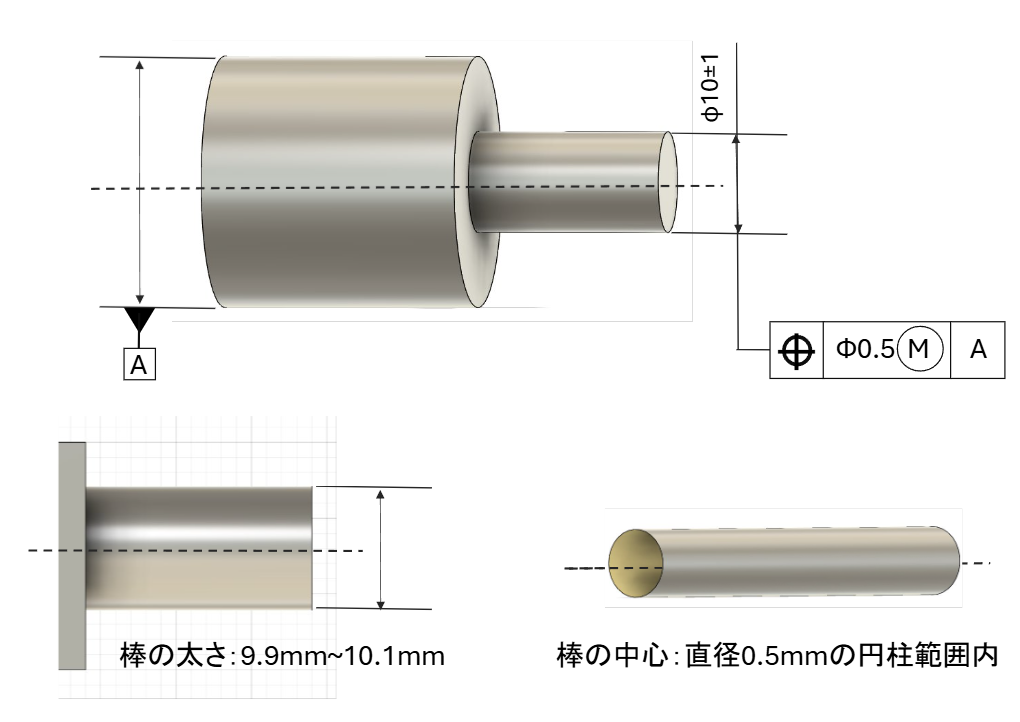
それではまず円柱を二つつなげた図形について、上記のような指示があったとします。
そのときに以下の条件を両方とも満たす必要があります。
- 右側の細い棒の太さが9.9mm~10.1mmの範囲である
- 右側の細い棒の中心はデータムAの中心線を基準とした直径0.5mmの円柱内にある
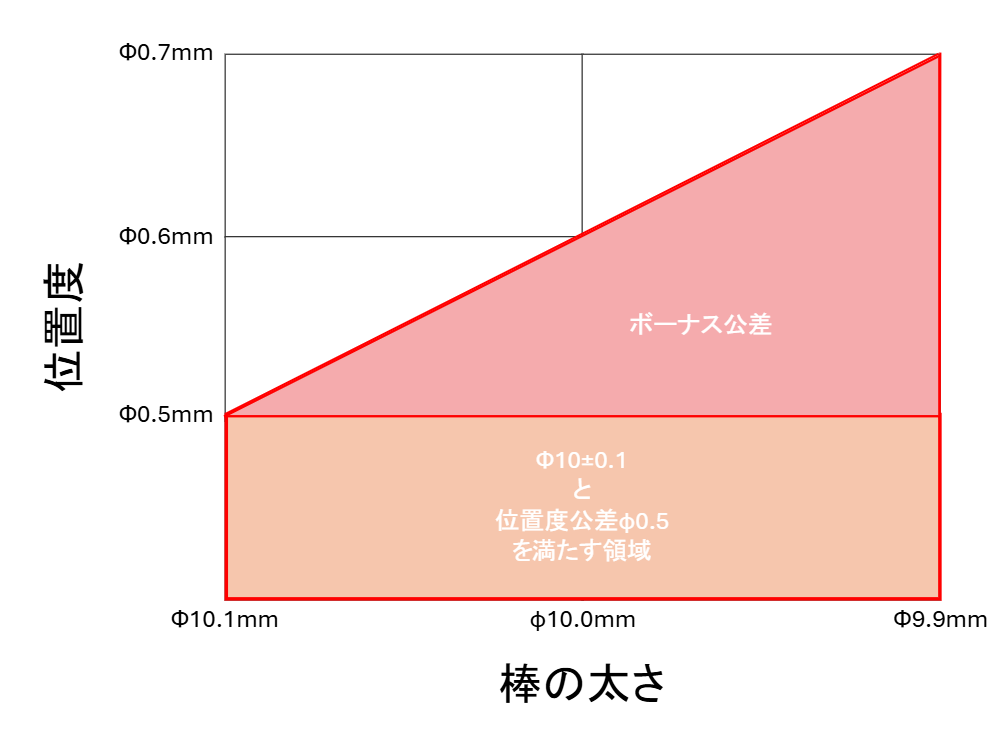
棒が10.1mmのとき
位置度公差はそのままΦ0.5になります。
この場合、棒を差し込む穴は最小でもφ10.1+φ0.5で「φ10.6mm」あればいいことになります。
棒が10.0mmのとき
棒の太さに余裕がφ0.1mm生まれました。その分ボーナス公差がφ0.1追加されます。
穴は最小で「φ10.6mm」なので、許される位置度公差がφ0.5→φ0.6に拡大します。
穴が9.9mmのとき
棒の太さに余裕がφ0.2mm生まれました。その分ボーナス公差がΦ0.2追加されます。
穴は最小で「φ10.6mm」なので、許される位置度公差がφ0.5→φ0.7に拡大します。
このように、棒の太さによって許される公差が変わっていきます。これがボーナス公差です。
ボーナス公差の具体例②
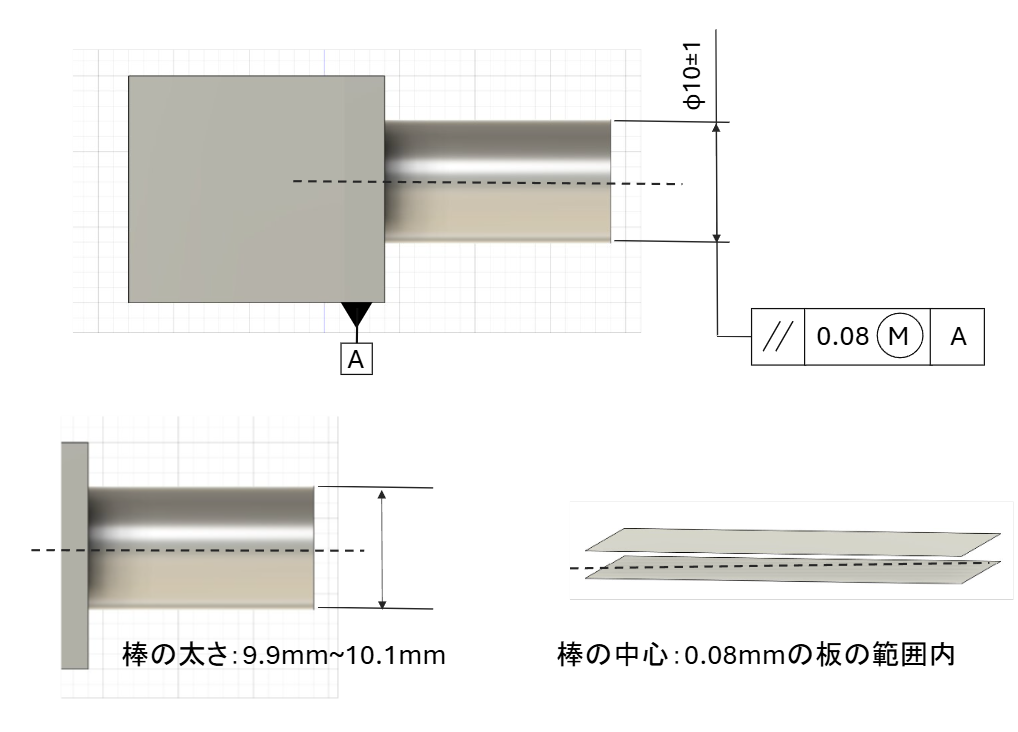
次に直方体に円柱をつなげた図形について、上記のような指示があったとします。
そのときに以下の条件を両方とも満たす必要があります。
- 右側の細い棒の太さが9.9mm~10.1mmの範囲である
- 右側の細い棒の中心はデータムAの面を基準とした0.08mmの板の間にある
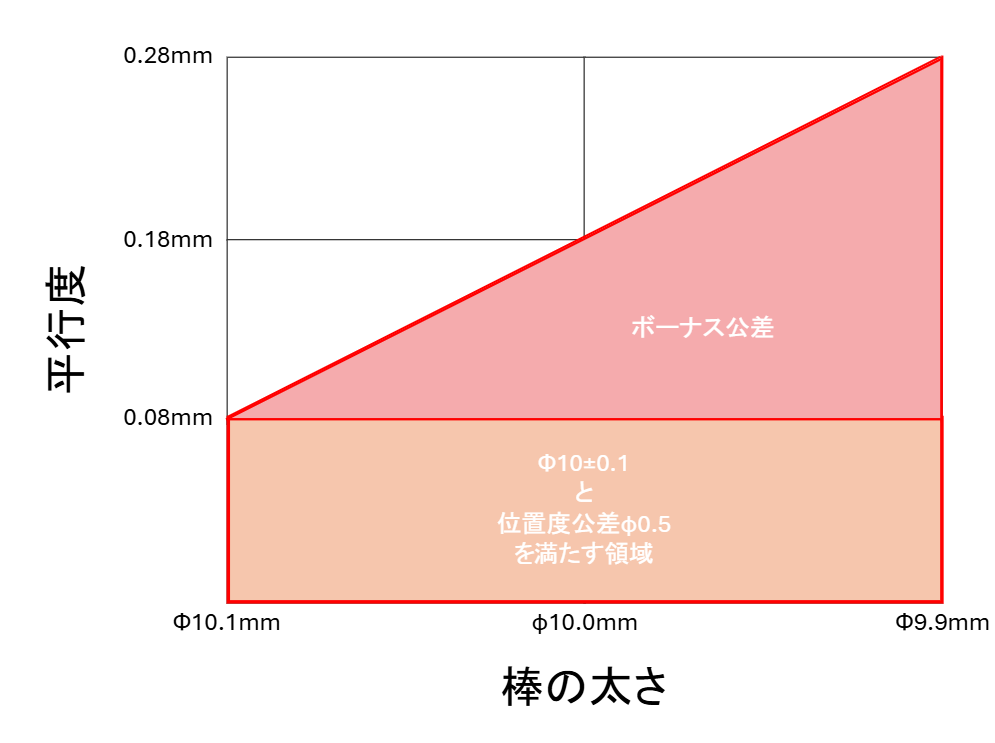
棒が10.1mmのとき
位置度公差はそのまま0.08mmになります。
この場合、棒を差し込む穴は最小でもφ10.1+φ0.08で「φ10.18mm」あればいいことになります。
棒が10.0mmのとき
棒の太さに余裕がφ0.1mm生まれました。その分ボーナス公差が0.1mm追加されます。
穴は最小で「φ10.18mm」なので、許される位置度公差が0.08mm→0.18mmに拡大します。
注意が必要なのは、今回はデータムA面に対する平行度なので、拡大するのはデータム垂直方向。
穴が9.9mmのとき
棒の太さに余裕がφ0.2mm生まれました。その分ボーナス公差が0.2mm追加されます。
穴は最小で「φ10.18mm」なので、許される位置度公差が0.08mm→0.28mmに拡大します。
注意が必要なのは、今回はデータムA面に対する平行度なので、拡大するのはデータム垂直方向。
このように、棒の太さによって許される公差が変わっていきます。これがボーナス公差です。
最大実体公差公式を使う場面
一般的に最大実体公差公式を用いるのは、部品同士のはめあいがメインですが、それ以外にも。
位置決めピンや穴の位置度管理
- ジグや治具で位置決めするピンや穴。
- 最大実体で正しく入るなら、それ以上にゆるくなった場合は「位置ずれしてもOK」とできる。
- このときボーナス公差が効いて製造が楽になる。
組立保証(機能ゲージ)
- 「ゲージ検査」でMMCは超便利。
- 例えば、部品がMMCで作られても規定のゲージに通れば、実際の組立でも必ず通る → 機能保証になる。
コストダウン
- 部品が必ずしも“カッチリ”じゃなくてよい場合、MMCを使うと余裕分がボーナス公差になる。
- 製造側が寸法精度を出しやすくなり、加工コストが下がる。





