
私の現在の研究分野は材料工学ですが、他の学問にも興味をもっていた時期もありました。
【材料工学】大学の学部「材料工学/材料科学」とは?特徴は?学べる大学も調べてみたよ
今回はその中でも特に面白いと感じた「量子論」「次元論」「無」について紹介しようと思います!
これらの学問は一見関係なさそうに見えますが、すべてが密接に関係しているのです。
量子力学
大学1年生の時に授業を聞いて感動したのを覚えています。
「光は粒であり波である」という驚くべき仮定から入ることもあり、挫折する学生もいるようです。
アニメや似非科学にも取り上げられがちで、名前は知っているという人も多いかもしれません。
光ってなんだ?

19世紀終わりに、物理学会において「光は粒であるか波であるか」という論争が巻き起こりました。
当時主流だった「波」として振る舞うという意見は、ヤングによる光の回折実験で証明されました。
一方でアインシュタインの光電効果をきっかけに、光を波だと考えると説明できないことが判明。
結果、光は”粒”としても”波”としても振舞う「光の二重性」という驚きの結論が導かれました!
一方で、”波”だと思われていた光が”粒”の性質を持つことを知ったド・ブロイは逆転の発想を得ます。
それは全ての物質はミクロな世界において、”粒”だけでなく”波”となる「物質波」という考え。
ミクロの世界では観測するまでは”波”として、観測すると”粒”としてふるまうと考えられています。
確率論の世界

観察するまで対象物の場所が確定せず、観測結果は確率論によるという考えは批判も巻き起こします。
全ては予測できるとされていた力学から見ると、確率論ではどんなに情報があっても予測できません。
アインシュタインは物理学が不完全なせいだと考え、「神はサイコロを振らない」と批判しました。
またこの確率論は、観測した瞬間に波は粒としてふるまうために、他の事象が一つに収縮します。
これは観測するまで物事が決まらないという意味で「シュレディンガーの猫」の反論も起こりました。
収束vs多世界理論
箱の中で同時に存在している猫は観測した瞬間にどうなるのかという問題が残ります。
これに対しコペンハーゲン学派は、複数ある確率が観察することで収束することを提唱しました。
しかしどんな要因で確率が収束するのか、観測の条件とは何なのかといった反論も多くありました。
それに対して重ね合わせをそのまま受け入れた考えが「多世界理論」です。
これは複数ある可能性は1つに収束するのではなく、世界のほうが分裂するという考えです。
多世界理論はSFにも取り込まれ、並行世界/パラレルワールドとして広く知られるようになりました。
次元論
ドラえもんの4次元ポケットは「空間3次元+時間1次元」のいわゆる「4次元時空」ではありません。
私たちの生活している「3次元空間」のほかに、さらに空間軸が存在すると考えるのが次元論です。
身近な低次元から見えない高次元へと考えを巡らせたり、未知の超立体を想像するのが楽しいです!
低次元から考える
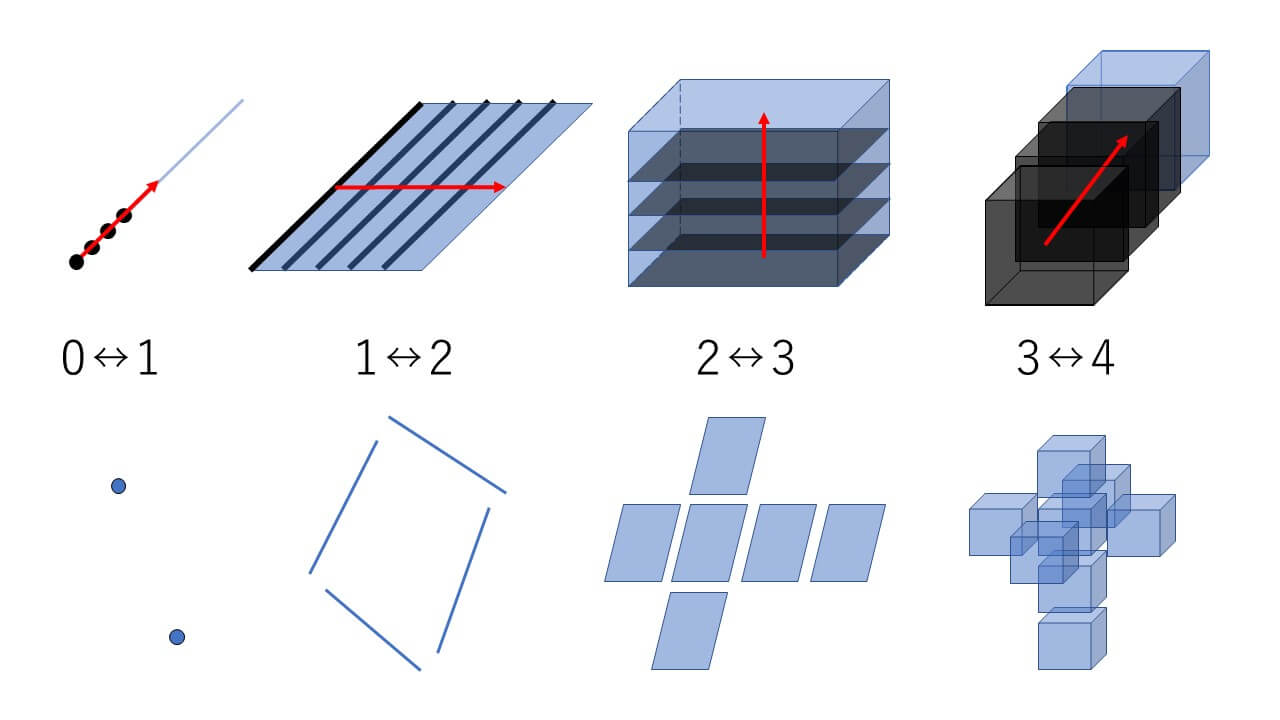
一つ目の考え方は図形をずらすことで次元を一つ上げる方法です。
0次元図形である「点」を第1軸に沿ってずらすと、1次元図形である「線分」になります。
1次元図形である「線分」を第2軸に沿ってずらすと、2次元図形である「平面」になります。
2次元図形である「平面」を第3軸に沿ってずらすと、3次元図形である「立体」になります。
この考えを利用すると、3次元図形を第4軸に沿ってずらすと4次元図形を得られます。
実際には第4軸は存在しませんが、このような考えから4次元を考えることができます。
二つの考え方は図形を分解することで次元を一つ下げる方法です。
3次元図形である「立方体」は、6つの2次元図形である「正方形」からできています。
2次元図形である「正方形」は、4つの1次元図形である「線分」からできています。
1次元図形である「線分」は、2つの0次元図形である「点」からできています。
予想によれば、4次元図形である「超立方体」は、8つの3次元図形である「立方体」からできるはず。
中途半端な次元
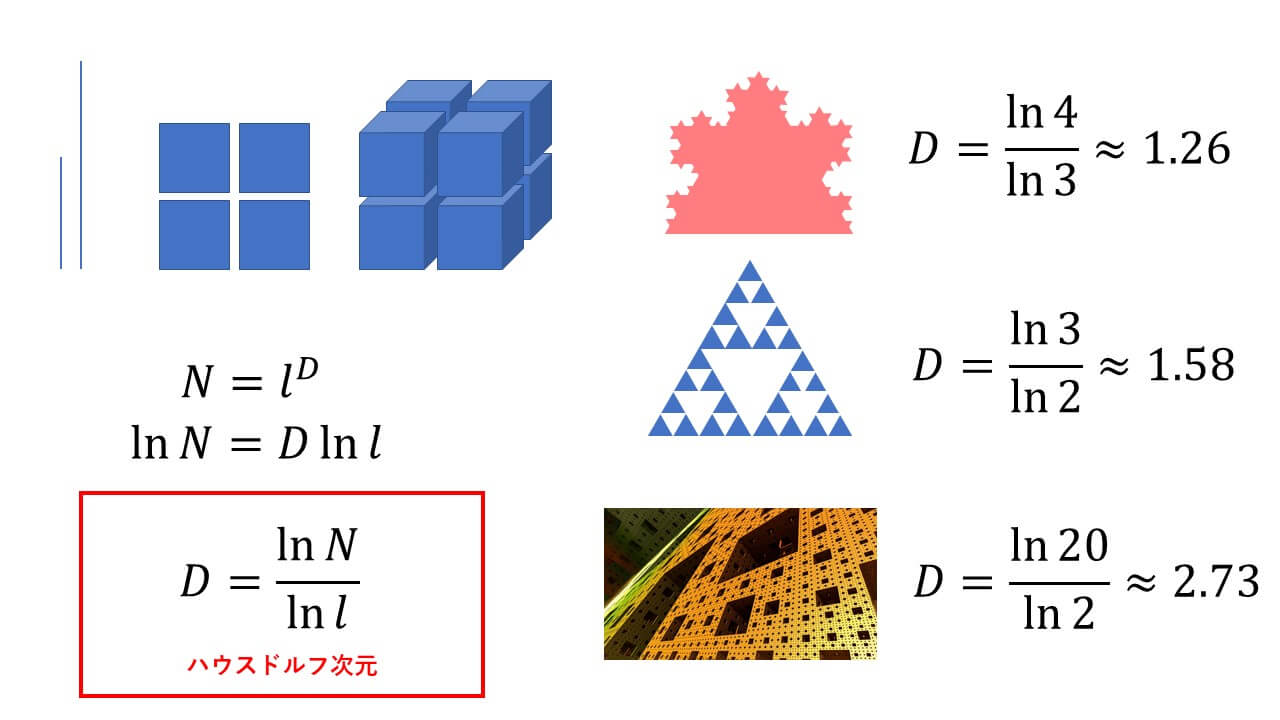
また1,2,3…と整数が多くみられる次元ですが、実は中途半端な次元も存在します。
そのためには以下のような「ハウスドルフ次元」を定義する必要があります。
「図形の辺をl倍拡大すると量がN^D倍になるとき、その量をn次元と定める」
例えば辺が2倍になると、線分は2=2^1倍、正方形は4=2^2倍、立方体は8=2^3倍になります。
ハウスドルフ次元において中途半端な次元を持つのが、ロマネスコで有名なフラクタル図形。
他にもコッホ曲線、シェルピンスキーのガスケット、メンガーのスポンジなどが知られています。
これらの図形はあくまで仮定上の図形や立体で現実には存在しませんが、面白い性質を持っています。
高次元とひも理論
現在、高次元空間の存在は多くの人に指示されており、中には11次元存在するという理論もあります。
実際には観察されていない高次元の存在が信じられている理由として、重力の存在があります。
この世界の力は一つの力から「電磁気力」「強い力」「弱い力」「重力」に派生したとされています。
しかし、この中でも重力だけが他の3つの力に比べて非常に弱いことが研究者を悩ませています。
理由として重力の一部は多次元に漏れているのではないかという突拍子もない説も。
他にも次元の最小単位は点でなく”ひも”であり、高次元空間は小さく折りたたまれているという説も。
これは超ひも理論と呼ばれ、量子力学などの矛盾なども解決できるかもしれないと期待されています。
無
ずっと疑問に思っていた「音がない」「味がない」「色がない」…は実際にものがないわけではない。
昔から真空には何があるのかということをずっと考えてきましたが、答えが得られませんでした。
何もない空間にあるものを考えると、無から宇宙ができたというトンデモ論も納得できるように。
段階的な無
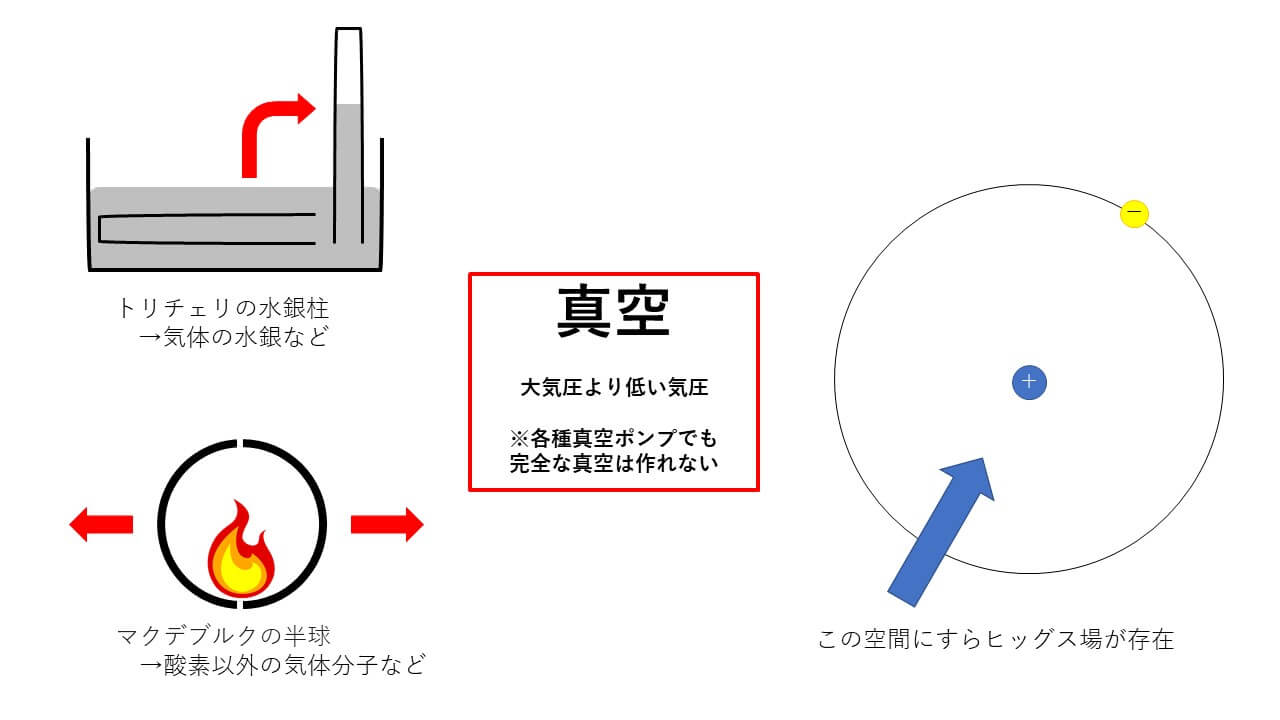
無と聞いて考えるのが「真空」ですが、これは大気圧より低い圧力の気体で満たされた空間です。
始めて真空を作り出したのは、水銀を使って大気圧を測定したトリチェリだと言われています。
彼は水銀の密度の高さを利用することで、空気のなかった筒から空間を生み出しました。
しかしこの真空は、厳密には気体になった水銀粒子などが含まれており、無ではありません。
ここからさらに粒子を取り除いていくことでも無を考えられそうですが、もっと簡単な方法も。
それは次に考える、水素原子における原子核と電子の間の空間です。
原子を構成する陽子と電子は最も小さな粒子であるはずなので、その間には何もないはずです。
しかし実際には、この空間にさえもヒッグス場というものが存在します。
これは光以外の物質のスピードを制限するもので、ヒッグス粒子として存在が確認されています。
「無」とは存在しない

あらゆる手段を用いてすべての粒子を取り除いたとしても完全な「無」はできません。
量子論におけるハイゼンベルグの不確定性原理により、エネルギーは完全な0になることができません。
何もない空間でもエネルギーが存在することは「カシミール効果」によって証明されています。
エネルギー状態は常に”揺らぎ”の状態にあり、何もない空間では粒子の対生成と対消滅が起こります。
エネルギーを波のようなものと考えると、常に揺らいで山と谷が生まれ消えてゆくようなものです。
エネルギーの波は場の量子論という考えによって素粒子として考えられるため、無は存在できません。
結論として、本当の意味で何もない「無」というのは我々の世界で作ることは不可能となっています。
本当の意味での「無」はないことから、何もない所から宇宙ができたビッグバン理論が導かれます。
現在は、宇宙はこのエネルギーの揺らぎが急激に膨張したことで誕生したと考えられています。
無にはいったい何があるのか
何もないはずの場所で力を伝える「場」を構築する素粒子にはいくつかの種類があります。
物質を構成するクォークとレプトン、それから力を伝達するゲージ粒子とヒッグス粒子です。
それぞれ電磁気力:光子、強い力:グルーオン、弱い力:ウィークボソン、重力:グラビトンに対応。
さらに何もないと考えられている空間には、素粒子の他にも物質があると考えられています。
ダークマターは、宇宙の総重量を計算した時に計算の合わない発見されていない物質です。
また宇宙の総エネルギーも計算が合わず、ダークエネルギーの存在も予想されますが、未発見です。
このように、無について考える以前に我々は存在するものにすら気づいていない事実があるのです。
全体的にふわっとした学問が好き
これらの学問は科学というよりも、不思議な現象として文系でも楽しめる内容になっています。
一方で数式での説明が難しいことから、トンデモ論や似非科学、宗教にも悪用されがちです。
わからないなりに勉強して理解を深めつつ、自己防衛にも努めることをおすすめします。

アニメもただ見るのではなく、わからないことに興味を持って調べると勉強になったりします。
今回はSFやファンタジー系のバトル作品に出てくる、中二病的な知識について調べてみました。
理系にとってはなじみやすい知識もあったりするかも、ぜひ読んでいってください!
シュレディンガーの猫
1935年にオーストリアの物理学者エルヴィン・シュレーディンガーが発表した物理学的実在の量子力学的記述が不完全であると説明するために用いた、猫を使った思考実験。
1/2の確率で放射能を出す物質とそれに反応して毒ガスが発生する装置を、猫とともに箱に入れます。
箱は外から見えず、ふたを開けるまでは猫が生きている状態と死んでいる状態が同時に存在します。
量子力学において結果は観測するまでわからないことのたとえに使われがちですが、実は違います。
ミクロの世界でのみあり得る法則のはずが、工夫次第でマクロの世界で起こってしまうという批判。
とある魔術の禁書目録では、この箱の中を観測する前に決定することができるのが能力者らしい。
パラレルワールド
ある世界(時空)から分岐し、それに並行して存在する別の世界(時空)を指す。並行世界、並行宇宙、並行時空とも言われている。
「平行世界」と間違えがちですが、並行は「ならんで進むこと/二つ以上のものが同時に行われること」
現在の世界とほとんど同じですが、ほんの少しだけ異なる世界が無数に存在しているという理論。
タイムパラドックスを説明する際、移動したのが過去ではなく並行世界であるという説明もできます。
基本的にパラレルワールド間の観測や干渉、ましては移動は不可能とされていますが果たして…?
ガンダム作品の多くはパラレルワールド、シュタインズ・ゲートでは「世界線」と呼称されています。
粉塵爆発
ある一定の濃度の可燃性の粉塵が大気などの気体中に浮遊した状態で、火花などにより引火して爆発を起こす現象である。
バトル系のラノベやアニメに登場しがちな攻撃方法で、有名なものには鉱山での事故があります。
可燃性粉塵、支燃物としての酸素、点火源(以上は燃焼の3要素)に加えて拡散状態、空間的制約。
この5つが粉塵爆発の条件で、粉塵が燃えやすいものでよく分散しているほど起こりやすいです。
酸化する(サビる、燃える)ものに関しては小さくすればするほど燃えやすくなるのもポイント。
そのため飛行機の持ち込み禁止物には、粉体や細かい鉄粉なども含まれていたりします。
レールガン
物体を電磁気力(ローレンツ力)により加速して撃ち出す装置である。
フレミング左手の法則の考え方を発展させ、金属レール上の物体を超音速で打ち出す装置です。
電力量などの課題も多いですが、実際に軍事関連で各国が研究を行っている実在する技術です。
武器以外としても、宇宙への輸送方法としても検討されメタルギアなどの作品にも登場します。
よく似た方式にコイルガンというものもあり、素人でもYoutubeの作成動画を見れば実現も可能。
ただ大電流やその殺傷性から、作ってみるときは自己責任で。
液体窒素
冷却された窒素の液体である。液化窒素とも呼ばれ液化空気の分留により工業的に大量に製造される。純粋な窒素が液相状態になったものである。
一般的に手に入る物質でおそらく最も温度が低いもので、名前の通り気体の窒素を冷やしたもの。
-196℃という低温という特徴のほか、常温で気体になると体積膨張と酸欠を引き起こすことが可能。
水と同じように気体は温度を下げると液体になり、ドライアイスは二酸化炭素を固体にしたもの。
研究用などでさらに温度を下げたいときは同じく気体のヘリウムを冷やした液体ヘリウムを利用。
同じく登場が多い絶対零度とは、熱の発生源である原子の振動が停止()する温度で-273℃のこと。
三位一体
キリスト教において父(=父なる神・主権)子(=神の子・子なるイエス・キリスト)霊(=聖霊・聖神)の三つが「一体(=唯一神・唯一の神)」であるとする教え。
宗教については詳しくないので、誤った知識を共有しないように抜粋だけにしておきます。
厨二病にとって宗教の話題は大好物、Wikipediaを読み漁った人間も多いのではないでしょうか。
個人的にキリスト教以外に多く登場するのはギリシャ神話、北欧神話な気がします。
ダークマター
天文学的現象を説明するために考えだされた仮説上の物質。”質量を持つ”、”物質とはほとんど相互作用せず、光学的に直接観測できない”、”銀河系内に遍く存在する”といった性質が想定される。
別名「暗黒物質」とも呼ばれており、存在が確認されたわけではなく説明のために仮におかれた物質。
星々を観察して宇宙の総量を計算したが、圧倒的に足りないことから暗黒物質の存在が仮定された。
光を発せず質量だけを持つという特徴を持つと考えられており、観測から存在が予測されている。
存在が全く謎であることから作品によってさまざまな考察が可能になっている。
とある魔術の禁書目録に登場する「未元物質(ダークマター)」は少し特徴が違う気がします。
ダークエネルギー
現代宇宙論および天文学において、宇宙全体に浸透し、宇宙の膨張を加速していると考えられる仮説上のエネルギーである。
ダークマターと同様に観察されていないが存在が預言されている未知のエネルギー。
宇宙の質量とエネルギーは、通常物質4.9%、ダークマター26.8%、ダークエネルギーが68.3%と算定。
宇宙は誕生当時から膨張を続けていることは観測結果から明らかだったが、そのエネルギーは不明。
現在はそのエネルギー源がダークエネルギーだと考えられている。











